数学笔记：勾股定理和三角函数

勾股定理: a²+b²=c²

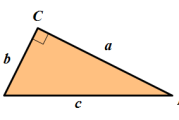
勾股定理: 如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么 a²+b²=c²

毕达哥拉斯的发现

证实勾股定理

赵爽指出：按弦图，又可以勾股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实。加差实，亦成弦实。

赵爽弦图证明勾股定理

赵爽所用的这种方法是我国古代数学家常用的“ 出入相补法 ” 。在西方，人们称勾股定理为毕达哥拉斯定理。

利用勾股定理做线段

勾股定理的证明

勾股定理的逆定理: 如果三角形的三边长a，b，c满足 a²+b²=c²，那么这个三角形是直角三角形。

古埃及人画直角

一般地，如果一个定理的逆命题经过证明是正确的，那么它也是一个定理，称这两个定理互为逆定理。

能够成为直角三角形三条边长的三个正整数，称为勾股数。

锐角三角函数

在Rt△ABC中，∠C=90°，我们把锐角A的对边与斜边的比叫做∠A 的正弦(sine)，记作sinA，即

sinA

∠A的邻边与斜边的比叫做∠A的余弦()，记作cos A，即

cosA

∠A 的对边与邻边的比叫做∠A 的正切()，记作 tan A，即

tanA

∠A 的正弦、余弦、正切都是锐角A的三角函数。

特殊的三角函数值

对于锐角A的每一个确定的值，sin A有唯一确定的值与它对应，所以sinA是A的函数。同样地，cos A，tan A 也是A的函数。

sin²60 °表 示(sin 60 °)²，即(sin 60°）·(sin 60°）。

解直角三角形

一般地，直角三角形中，除直角外，共有五个元素，即三条边和两个锐角。由直角三角形中的已知元素，求出其余未知元素的过程，叫做解直角三角形。

在Rt△ABC中，∠C为直角，∠A，∠B，∠C所对的边分别为a，b，c，那么除直角∠C外的五个元素之间有如下关系：

(1)三边之间的关系:

a²+b²=c²（勾股定理）

直角三角形边角关系

解直角三角形题型