高考数学果盘 =gt; 核心知识

　　三数（数列，书里统计，函数）两何（立体几何包括平面几何，解析几何）两三角（解三角形，三角函数性质）。

　　极坐标，参数，实际应用不可少（包括新定义一些概念函数，题中给出)

　　归纳如下；

　　三数两何两三角，极坐标,参数，实际应用来参考。

　　基本就这些知识，但是考试出题也蛮复杂的透过现象看本质,其实要考出好成绩总结知识点如下

　　第一重要的是向量知识，

　　第二是一元二次方程求根公式；

　　第三是三角函数的各种变化包括解三角形；

　　第四是函数知识，考核函数要考核复合函数的考核办法，

　　懂的函数性质分析的归纳总结一般规律；

　　第五数列递推分型，拆项，换元构造数列，以及错位相减的那些常见方法；

　　绝对值不等式，和一些导数正负的判断，参数对导数的决定或影响；

　　第六解析几何的参数归纳，量化参数个数，联立方程分秒决断；

　　数理统计数学期望分事件，乘法分步加法算，

　　技巧如下1穿根对函数单调性的秒断；

　　2已知离心率求三参的平方比是求解的最佳，且可三个参数转化一个参数。

　　一般说来联立两个方程比较好，其他参数转化一下，免得面太大难以把握。

　　3 数列的错位相减法是分子等差，分母等比，此为应用条件。

　　4求欧米茄角速度也就是三角函数变量X的系数，考核区间参考对称中心，求半个周期，再求角速度

　　有时题中区间并不是关于中点对等，易错点；

　　5 函数应用一个是分段函数，在一个是列方程消变量构造函数的问题，都是二元转化一元函数。

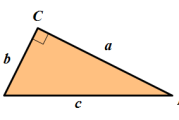
　　6解三角形，正旋余玄定理用来转化边和角，积化和差二倍角，利用平方关系或者基本不等式求极值。切炫转化。

　　函数知识技巧，

　　A切线问题导数函数赋值就搞定了

　　B单调分析》导数》0》驻点=导数零点》参数作为导函数的根参与根的排序》先讨论参数在讨论变量》导数的正负用穿根法判断》函数的单调》赋值》极值的判断》函数值的正负或者极限》

　　C构造函数是不等式的恒成立问题还是函数分析，方法同上，极值处的函数值是分析的重点。

　　懂得这些技巧才知道数学的皮毛，逻辑思维要求做出快速的判断

　　高考就是奖赏那些下苦功夫的人，其实题目并不难，但是做好了就需要每天2个小时的数学学习。

　　比如线段定比分点的内分点和外分点的比值有怎样区别，精细的东西做好了才能驾驭自己的技巧

　　再比如余玄定理有几种证明方法。解析法，向量法，三角函数转化高的勾股定理法

　　立体几何求向量直接利用射影求边长，先求出长度在确立方向，不必求点的坐标这样做节约时间。

　　立体几何求向量 先求长度后定向.法向量坐标于已知向量的坐标关系是组成的三阶行列式的代数余子式的坐标

　　【 1 2 3】

　　【 4 5 6 】 x= (2 3 y=-( 1 3 z=(1 2

　　【 x y z 】 5 6 ) 4 6 ) 4 5)

　　这是三阶行列式和代数余子式结果，立体几何法向量坐标结果，三个坐标可以被公约数约去也可正负转化，因为法向量是2个方向，要摸是夹角，要摸是其补角。

　　其零散的知识，什么同增异减，总之参加考试发挥还坏在于方法学，比如解三角形如果已知条件是已知一个角，其他两个角就可以互化，转化为一个变量的方程问题。常识性的技巧就是看题少做题。